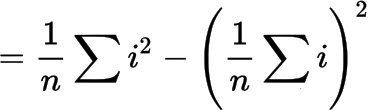I’ve been asked to expand on this point:
Easier to prototype ideas. For example, you can use functional programming to solve problems that are harder to express using imperative programming.
Lisp allows you to write in either a functional or imperative style, or a mixture of the two.
As an example of what functional and imperative mean, here’s the same problem approached in an imperative and functional style.
Suppose we want to calculate the variance of a set of data values:
1 4 9 16 25 36 49
We can use the equation:
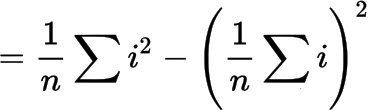
Imperative
Here’s the imperative approach. For convenience we first define a sq function:
(defun sq (x) (* x x))
The imperative version is like a recipe. We set up the three variables n, sum, and sumsq, and then step through the data a value at a time, updating the three variables:
(defun variance-i (data)
(let ((n (length data))
(sum 0)
(sumsq 0)
d)
(dotimes (i n)
(setq d (nth i data))
(setq sum (+ sum d))
(setq sumsq (+ sumsq (sq d))))
(- (/ sumsq n) (sq (/ sum n)))))
This is almost exactly how you would express the program in an imperative language such as C or C++:
const int ndata = 7;
float dataset[ndata] = {1, 4, 9, 16, 25, 36, 49 };
float variance (float* data, int n) {
int sum = 0, sumsq = 0;
for (int i=0; i<ndata; i++) {
float d = data[i];
sum = sum + d;
sumsq = sumsq + sq(d);
}
return sumsq/n - sq(sum/n);
}
Let’s check that it works:
> (variance-i '(1 4 9 16 25 36 49))
268
Functional
Now the functional approach. This approach consists of building up a series of functions that produce each of the intermediate results that we need. The functions n and sum each take a list of numbers, and return the number of values in the list, and the sum of those values, respectively:
(defun n (data) (length data))
(defun sum (data) (apply + data))
The function squares takes a list of numbers and returns a list containing the square of each number:
(defun squares (data) (mapcar sq data))
Now we are in a position to write the function variance :
(defun variance-f (data)
(- (/ (sum (squares data)) (n data))
(sq (/ (sum data) (n data)))))
Note that the function variance-f is a direct expression of the definition of variance. We haven’t had to construct a recipe to calculate the variance.
Again, testing the function:
> (variance-f '(1 4 9 16 25 36 49))
268