Another collection of uLisp puzzles – with answers

[johnsondavies]

Keeping up the tradition I started last year with A small collection of uLisp challenges, here is a collection of amusing uLisp problems to challenge your brain cells at this festive time of year. I’ll give the answers in ten days’ time.

A number trick

Here’s a hexadecimal number trick you can try with a 32-bit copy of uLisp, such as the versions for ARM, ESP32, or STM32 boards (or a copy of Common Lisp).

• Think of any three-digit hexadecimal number.

To demonstrate the trick we’ll use #xABC, but you should choose a different one.

• Write it twice; so our number now becomes: #xABCABC.
• Set it to a variable, with a command such as:

> (defvar n #xABCABC)
n

• Divide it by #x11, using truncate to ignore any remainder:

> (setq n (truncate n #x11))
662268

• Now divide it by #xF1, again ignoring any remainder:

> (setq n (truncate n #xF1))
2748

The final result is 2748.

Now see what the decimal value of your original hex number was:

> #xABC
2748

Amazingly it’s the same result! How does this work?

A strange recursive function

This unusual recursive function r is defined as follows for non-negative values of n:

r(n) = n + (n & r(n-1))

where & is the bitwise logical AND operation.

Its behaviour is quite erratic; for example:

r(336) is 672, but r(337) is 337.

How can you implement the function in Lisp?

A deceptively simple maze

This is a more difficult variant of the Tweetmaze I described in the uLisp examples:

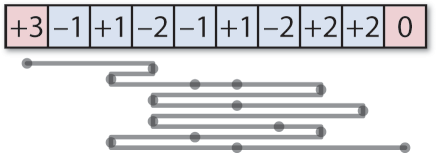
In this “Offset Tweetmaze” you start from the ‘+3’ on the left, and the aim is to find a route to the ‘0’ on the right in the smallest number of left or right jumps.

The number on each square tells you how the size of your jump changes. The starting number is +3, so initially the length of your jumps is 3, and your only choice is to jump three cells to the right.

You land on a cell marked -2 so now the length of your jumps is reduced to 1, and you have a choice of jumping one cell to the left or one cell to the right from that cell. Note that negative jumps aren’t allowed.

Continue in this way and find the smallest number of jumps that will take you to the rightmost cell.

Try and solve this maze by hand. Then check your solution by writing a uLisp (or Common Lisp) program to solve it; you might find the original Tweetmaze program useful as a starting point.

Converting kilometers to miles

Suppose you are developing a GPS-based program in uLisp that will display the distance travelled, in km or miles, on a 7-segment display. The kilometer display will handle up to 32767 km. However, we also want the option of displaying the distance in miles, which involves dividing this value by 1.609344. The problem is that you’re using an 8/16-bit platform, which only handles signed 16-bit integers in the range -32768 to +32767.

The task is to write a function km-miles that will convert its argument from km to miles using 16-bit integer arithmetic, and get the result accurate within a mile over the whole range 0 to 32767 km.

For example, your function should convert 23456 km as follows:

> (km-miles 23456)
14575

Hint: a good approximation to 1.609344 is 103/64.

Interpreting a 16-bit value as signed

There are versions of uLisp running with both 16-bit signed integers and 32-bit signed integers.

Suppose you have a 16-bit value representing a signed integer. On a 16-bit version of uLisp the value will automatically be interpreted as a signed integer; for example:

> #xFFFF
-1

However, on a 32-bit version of uLisp it will be interpreted as a 32-bit signed integer:

> #xFFFF
65535

In this case you can use the following function to convert it:

(defun s16 (d)
  (- (logand d #x7FFF) (logand d #x8000)))

For example:

> (s16 #xFFFF)
-1

However, this function gives arithmetic overflow on an 8/16-bit platform.

What if you want a routine that will work identically, irrespective of whether it’s running on an 8/16-bit or 32-bit platform? This is a common problem when interpreting the values from peripherals, such as sensors.

Design a uLisp function that treats its argument as a 16-bit signed integer, independently of the platform it’s running on. In other words:

(s16 #xFFFF)

should return -1 on both 8/16-bit platforms and 32-bit platforms.

Happy puzzling!

[johnsondavies]

Here are the answers to the uLisp challenges.

A number trick

The trick involved writing a three-digit hexadecimal number, such as #xABC, twice to give #xABCABC.

Then, after dividing it successively by #x11 and #xF1, ignoring remainders, the result turned out to be equal to the original number. How?

Writing a hexadecimal number twice is equivalent to multiplying it by #x1001. This number in decimal is 4097, which factorises into the prime factors:

17 x 241.

#x11 is 17 and #xF1 is 241, so dividing by #x11 and #xF1 is equivalent to dividing by #x1001, which clearly will get you back to the original number.

This is a hexadecimal version of an old trick in which you write a three-digit decimal number twice, and then divide by 7, 11, and 13. That one works because writing a decimal number twice is equivalent to multiplying it by 1001, and 1001 = 7 x 11 x 13.

A strange recursive function

I proposed an unusual recursive function r defined as follows for non-negative values of n:

r(n) = n + (n & r(n-1))

where & is the bitwise logical AND operation.

Most recursive definitions need a base case, which will stop the function recursing for ever. In this case the base case is implicit in the fact that when n is zero, (n & r(n-1)) is zero irrespective of the value of r(n-1), so we can deduce that r(0) = n.

To implement the function in Lisp you need to make the base case explicit:

(defun r (n)
  (cond
   ((zerop n) n)
   (t (+ n (logand n (r (1- n)))))))

Now we can confirm:

> (r 336)
672

> (r 337)
337

A deceptively simple maze

The problem was to solve this more difficult variant of the Tweetmaze I described in the uLisp examples:

In this Offset Tweetmaze you start from the ‘+3’ on the left, and the aim is to find a route to the ‘0’ on the right in the smallest number of left or right jumps. You start with a jump of length 3, and the number on each subsequent square tells you how the size of your jump changes.

The shortest solution consists of 15 jumps; well done if you solved it by hand!

The task was to modify the Tweetmaze program to solve this type of maze. Here’s the modified version of the program:

(defun sol (maz &optional (que '(((0 0)))))
  (let ((go (- (length maz) 1)))
    (if (= (caaar que) go) 
        (reverse (mapcar #'first (car que)))
      (let* ((top (pop que))
             (pos (first (first top)))
             (jmp (second (first top)))
             (off (+ jmp (nth pos maz)))
             (rt (+ pos off))
             (lt (- pos off)))
        (when (and (> off 0) (>= lt 0))
          (setq que (append que (list (cons (list lt off) top)))))
        (when (and (> off 0) (>= rt 0) (<= rt go))
          (setq que (append que (list (cons (list rt off) top)))))
	(sol maz que)))))

This extends the original Tweetmaze program by representing the two positions we can jump to at each stage as a list consisting of the number of the square lt (for a move to the left) or rt (for a move to the right), and the current jump size, off .

To solve the maze we do:

> (sol '(+3 -1 +1 -2 -1 +1 -2 +2 +2 0))
(0 3 2 4 5 7 3 5 8 3 6 7 4 2 5 9)

Here’s an illustration of the solution:

The solver could be made more efficient, by discounting squares you’ve already visited in the same state, but it’s adequate for a simple maze like this.

Here’s another Offset Tweetmaze to try:

Converting kilometers to miles

The problem was to convert a distance from kilometers to miles, using signed 16-bit integer arithmetic, such that the result is accurate to within a mile over the whole range 0 to 32767 km.

We can take advantage of the fact that a good approximation to 1.609344 is 103/64.

What we effectively want to calculate is:

(setq miles (/ (* km 64) 103))

However, this will overflow for values of km greater than 511.

The trick is to try doing the multiplication and division in the opposite order:

(setq try (* (/ km 103) 64))

There’s now no danger of overflow, but the result is a step function that’s only correct if km is a multiple of 103.

However we can fix this by adding on a correction to interpolate between the steps, as follows:

(setq correction (/ (+ (* (mod km 103) 64) 51) 103))
(setq miles (+ (* (/ km 103) 64) correction))

The correction is rounded to the nearest integer by adding 51 before dividing by 103.

The largest value that:

(mod km 103)

can have is 102, so we can be sure this won’t overflow because 102 x 64 + 51 is less than 32767. In general, we can use this technique to multiply by any rational number a/b provided a+b is less than 32767.

Here’s the whole function:

(defun km-miles (km)
  (let* ((correction (/ (+ (* (mod km 103) 64) 51) 103))
         (miles (+ (* (/ km 103) 64) correction)))
    miles))

For example:

> (km-miles 23456)
14575

This may be a standard technique, but I’ve never seen it written about before.

Interpreting a 16-bit value as signed

The problem was to find a function that interprets a 16-bit value as a signed 16-bit integer independently of whether the platform works with signed 16-bit integers, or signed 32-bit integers.

One approach is to use a conditional to test bit 15 of the number, and if it’s a ‘1’ subtract 32768 from the bottom 15 bits of the number:

(defun s16 (d)
  (if (zerop (logand d #x8000)) d (+ (logand d #x7FFF) -32768)))

Note that we can’t just say:

(- (logand d #x7FFF) 32768)

because 32768 will cause overflow.

Here’s a simpler and more elegant solution:

(defun s16 (d)
  (- d (ash (logand d #x8000) 1)))

With 16-bit signed integers:

(ash (logand d #x8000) 1)

will always be zero, so d is returned unaffected.

With 32-bit signed integers the expression evaluates to 65536 when bit 15 is a ‘1’, so subtracting that from d effectively subtracts the value of that bit and subtracts 32768.