Are you one of the 10% of competent programmers?

#1

I recently discovered this article on Colin Wright’s blog about using Binary Search as an interesting test problem: Binary Search Reconsidered.

The algorithm is:

You’re looking for an item in a sorted list, so you look in the middle. If the thing you find is bigger than what you’re looking for, then the item - if it’s there at all - must be in the first half, otherwise it’s in the second half. Repeat until you either find the item, or there are no items left in which case the item is not in the list.

In his book Programming Pearls Jon Bentley wrote that he assigned this problem in courses at Bell Labs and IBM. Professional programmers had a couple of hours to convert the above description into a program in the language of their choice.

At the end of the specified time, almost all the programmers reported that they had correct code for the task … but on testing their code 90% of the programmers found bugs in their programs.

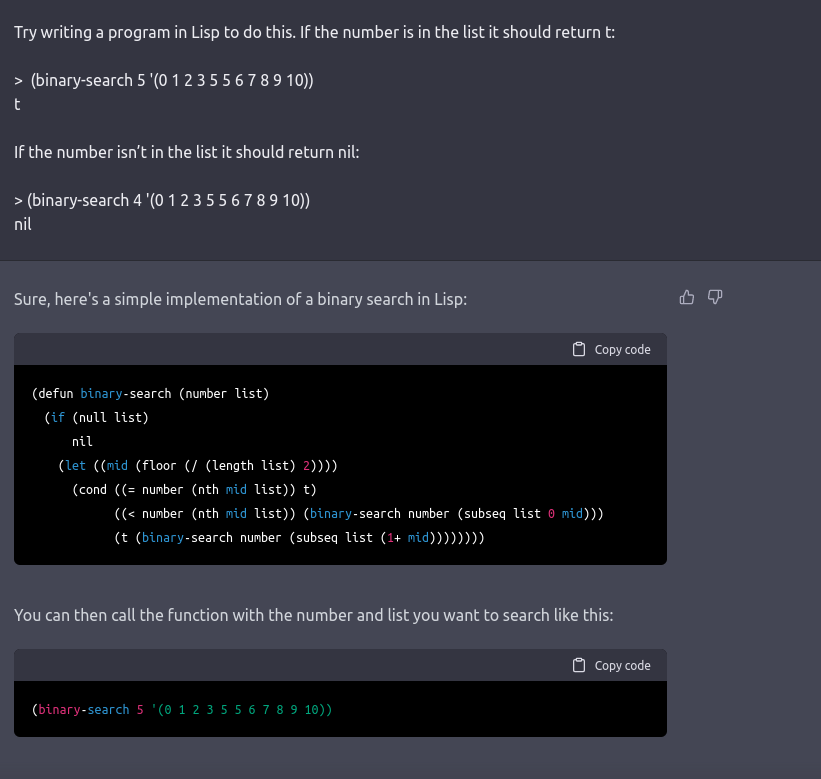
Try writing a program in Lisp to do this. If the number is in the list it should return t:

>  (binary-search 5 '(0 1 2 3 5 5 6 7 8 9 10))
t

If the number isn’t in the list it should return nil:

> (binary-search 4 '(0 1 2 3 5 5 6 7 8 9 10))
nil

You’re not allowed to test the program until you’ve finished it.

I wrote my program in uLisp, but I have to admit that my program had a silly mistake so I’m in the 90%. I’ll reveal my answer in this thread in a day or so.

See how well you get on!

#2

Very nice excercise. Thanks.
Had to break out of an infinite loop on the first try… :^)

An idea would be to restate the problem to search an array, because it feels wrong to use lists for this.
Even checking the size of the list is already traversing the whole list, and a simple (member n lst) would outperform the binary search when using lists.
Using arrays we can really show off both the beauty and speed of Lisp.

But still a very good brain-teaser.
And thanks for uLisp.

#3

Yes, good point about lists vs. arrays. I did it using lists and that made it a lot easier.

#4

Hmm, that makes me very curious about your solution.
In my solution, the only difference between using list and array is changing nth to aref.

Just had to tweak it to support both lists and arrays. ;)
Works in both uLisp and Common Lisp.

Would you like us to post solutions? Or maybe wait a while?

#7

Here’s my solution to the Binary Search algorithm, in uLisp:

(defun binary-search (item lst)
  (cond
   ((null lst) nil)
   (t (let* ((index (truncate (length lst) 2))
             (mid (nth index lst)))
        (cond
         ((= item mid) t)
         ((< item mid) (binary-search item (subseq* lst 0 index)))
         (t (binary-search item (subseq* lst (1+ index)))))))))

(defun subseq* (lst n &optional (m (length lst)))
  (cond
   ((> n 0) (subseq* (cdr lst) (1- n) (1- m)))
   ((zerop m) nil)
   (t (cons (car lst) (subseq* (cdr lst) 0 (1- m))))))

If it hasn’t found the item it recursively calls binary-search on the first half of the list, or the second half of the list, depending on whether the item is less than or greater than the middle element of the list.

In uLisp subseq doesn’t work with lists, so I’ve defined my own version of subseq called subseq*. In Common Lisp you can just use subseq.

I look forward to seeing what other solutions anyone has come up with!

#8

90%, unfortunately… and my godawefully ugly solution, merely to satisfy the description but without any regard to optimization (just called it “ispresent”):

(defun ispresent (x srtl)
  (cond
   ((null srtl) nil)
   ((null (cdr srtl)) (equal (car srtl) x))
   (t (let ((lensrtl (length srtl)))
        (let ((halflen (floor (/ lensrtl 2))))
          (let ((firsthalf (reverse (nthcdr halflen (reverse srtl))))
                (secondhalf (nthcdr (- lensrtl halflen) srtl)))
            (cond
             ((or (equal (car (last firsthalf)) x) (equal (car secondhalf) x)) t)
             (t (or (ispresent x firsthalf) (ispresent x secondhalf))))))))))
#9

It seems to work OK! Note that it needs a few extra definitions to work in uLisp.

#11

Another 90%-er… :-\

(defun binary-search (x sortl)
    (let ((bsrch (lambda (num start end)
		(let ((mid (+ start (floor (- end start) 2))))
		    (cond
			   ((> start end)			nil)
			   ((= num (nth mid sortl))	t)
			   ((< num (nth mid sortl))	(bsrch num start (- mid 1)))
			   (t				(bsrch num (+ mid 1) end))
		    )))))
     (bsrch x 0 (- (length sortl) 1))
))
#12

Hello,

Just for fun I asked chatGPT:

Screenshot%20from%202023-01-27%2016-33-48
Screenshot from 2023-01-27 16-33-48.png821x779 46.7 KB

best regards

#13

Here is an iterative implementation similar to what one might write in an imperative language.

(defun binary-search (n lst)
  (let*
      ((f 0)
       (b (1- (length lst))))
    (loop
     (when (> f b) (return nil))
     (let*
         ((c (truncate (+ f b) 2))
          (v (nth c lst)))
       (cond
         ((= n v) (return t))
         ((< n v) (setq b (1- c)))
         (t       (setq f (1+ c))))))))

Assuming it’s working, which I wouldn’t bet either way, it worked “first time.” Full disclosure: I read Bentley’s Programming Pearls books years ago and have implemented the algorithm a few times in other languages.

#14

@johnsondavies Correct me if I’m wrong but… the reason that my version of binary-search works on uLisp and not on Common Lisp is that you’re keeping symbols for defvar and defun in the same lookup table and CL does not? TNX!
-Rusty-

#15

Yes, in Common Lisp you have to write it as:

(defun binary-search (x sortl)
  (labels
      ((bsrch (num start end)
         (let ((mid (+ start (floor (- end start) 2))))
           (cond
            ((> start end)           nil)
            ((= num (nth mid sortl)) t)
            ((< num (nth mid sortl)) (bsrch num start (- mid 1)))
            (t                       (bsrch num (+ mid 1) end))))))
    (bsrch x 0 (- (length sortl) 1))))
#16

I thought I would get an email when there was something happening in this thread, but nothing, so a bit late with my contribution…

Anyway, I really like your very Lispy recursive solution. Beauty.
It also makes interesting patterns when both functions are traced with a proper input length.
And it’s much faster than I thought it would be, even when tracing. I’m using Pico W’s.

My uLisp solutions, one looping and one recursive - that also work in Common Lisp - handle both arrays and lists:

(defun binary-search (num seq)
  "Loopy - array or list"
  (let ((lo 0)
        (hi (1- (length seq))))
    (loop
      (when (< hi lo) (return))
      (let* ((pos (ash (+ lo hi) -1))
             (val (if (listp seq) (nth pos seq) (aref seq pos))))
        (cond
          ((< num val) (setf hi (1- pos)))
          ((> num val) (setf lo (1+ pos)))
          (t (return t)))))))

(defun binary-search (num seq &optional lo hi)
  "Recursive - array or list"
  (if (null lo)
      (binary-search num seq 0 (1- (length seq)))
      (when (<= lo hi)
        (let* ((pos (ash (+ lo hi) -1))
               (val (if (listp seq) (nth pos seq) (aref seq pos))))
          (cond ((< num val) (binary-search num seq lo (1- pos)))
                ((> num val) (binary-search num seq (1+ pos) hi))
                (t))))))

Also made some helper functions for testing that work both in uLisp and Common Lisp:

(defun fill-array (n &optional skip)
  (let ((v (make-array n)))
    (dotimes (i n v)
      (setf (aref v i) (if (eq i skip) (1+ i) i)))))

(defvar vt (fill-array 10 4))
(defvar vf (fill-array 50 4))
(defvar vh (fill-array 100 4))

(defun fill-list (n &optional skip)
  (let (l)
    (reverse
     (dotimes (i n l)
       (push (if (eq i skip) (1+ i) i) l)))))

(defvar lt (fill-list 10 4))
(defvar lf (fill-list 50 4))
(defvar lh (fill-list 100 4))

I was also playing with the idea of recursively splitting the input, like you did, because that felt like the naturally Lispy way, but only did that solution for arrays in Clojure:

(defn binary-search [num v]
  "Search for num in array v"
  (let [cnt (count v)]
    (when (pos? cnt)
      (let [pos (bit-shift-right cnt 1)
            val (v pos)]
        (cond (< num val) (recur num (subvec v 0 pos))
              (> num val) (recur num (subvec v (inc pos)))
              :else true)))))

Nice exercise.
Thanks.

#17

Thanks for the contributions! By the way, the Discourse syntax highlighting doesn’t work properly for “lisp” or “clojure” so I tend to use “text”.

#18

Ah, I see. Thanks for fixing that.